ما هي الاعداد الأولية وكيفية تحديد العدد الأولي

الاعداد الأولية هي أعداد صحيحة موجبة لا تقبل القسمة إلا على العدد واحد وعلى نفسها فقط، ومن أبرز خصائص الأعداد الأولية أن العددان (0 , 1) لا يندرجان ضمن قائمة الأعداد الأولية، وأي رقم ينتهي بالعدد ( 0, 5) مثل (25, 30) فهو عدد غير أولي، والعدد 2 أصغر عدد أولي بالرغم من أنه عدد زوجي، وكل مضاعفات العدد 3 هي أعداد غير أولية.
- أنشئ المختص بعلم الرياضيات جولد شتاين ومعه علماء آخرون قائمة أول خمسة وعشرين عددًا أوليًا، في تسلسل تلك الأعداد له أهمية في مجال دراسة العدد الأولي لتحديد كيفية الاستفادة منهم .
- تم اقتراح بعضاً من النظريات مع براهينها لتوليد التسلسل (على سبيل المثال الفكرة الأولية في التصنيف المثالي ونظرية الأولية للتقدم الحسابي) .
- إثبات GoldBachs وتستند فرضيته إلي نظرية التخمين وخاصية قطرية الفجوة، والتي تتكون من الأعداد الصغيرة وأخرى كبيرة.
- بالإضافة إلى اقتراح خوارزمية رقم أولي أخر بواسطة Riesel و Hans، حيث يُعتبر p عددًا أوليًا كاملاً.
- مساهمة LU في توليد تلك الأعداد، هي أنه يُمكن وضع الصحيحة الموجبة بمجموع العدد الأولي.
- في حين أن إم وولف في اقتراح خوارزمية أخرى لتوليد عدد أولي، حيث أثبت أنه يُمكن الحصول عليه من المجموع التربيعي لها.
- غيرهم اقترح أن الأعداد الكبيرة ناتج عن جمع عدد وحاصل تكعيب من أربعة أعداد أولية.
محتوى المقال
- 1 ما هي الاعداد الأولية
- 2 الأعداد الأولية من 1 إلى 20
- 3 الأعداد الأولية من 1 إلى 1000
- 4 هل الواحد عدد أولي
- 5 الأعداد الأولية من 1 إل ى 10
- 6 الأعداد الأولية من 1 إلى 30
- 7 الأعداد الأولية الفردية
- 8 هل 2 عدد أولي
- 9 أسهل طريقة لمعرفة العدد الأولي
- 10 التشفير والأعداد الأولية
- 11 أمثلة حول الأعداد الأولية والمُركبة
ما هي الاعداد الأولية
الأعداد الأولية هي الأعداد الطبيعية الأكبر من الواحد، والتي تقبل القسمة على نفسها وعلى العدد واحد فقط.
- مثال على ذلك: العدد 13، هو عدد يقبل القسمة على نفسه 13 ÷ 13 = 1، كما أنه يقبل القسمة على العدد 1 بمعنى 13 ÷ 1 = 13
- بينما الأعداد المركبة؛ فهي تقبل القسمة على عدة عوامل مثل العدد (28) والذي يعتبر عدد غير أولي.
- تجدر الإشارة إلى أن العددان ( 1، 0) أعداد ليست أولية وليست مركبة، ويعد العدد (2) هو أصغر عدد أولي بالرغم من أنه عدد زوجي، لأنه لا يقبل القسمة إلا على نفسه وعلى العدد واحد، ويعتبر العدد ( 2 ) هو العدد الأولي الزوجي الوحيد.

الأعداد الأولية من 1 إلى 20
الأعداد الأولية يقصد بها الأعداد الموجبة الصحيحة الأكبر من واحد، وهي التي تقبل القسمة على العدد واحد وعلى نفسها، ويعتبر العددان 1، 0 أعداد غير أولية.
الطريقة الأولى
- أبسط طريقة لاستخراج الأعداد الأولية من الرقم ( 1 : 20) هي أن كل الأرقام الفردية التي تنحصر بين الأعداد من (1 : 20 ) هي أعداد أولية ما عدا العدد ( 1 )؛ فهو عدد غير أولي.
- تجدر الإشارة إلى أن العدد ( 2 ) يعتبر من ضمن الأعداد الأولية بالرغم من أنه عدد زوجي، وذلك لأنه لا يقبل القسمة إلا على نفسه وعلى العدد واحد.
- بذلك؛ يمكن معرفة الأعداد الأولية المحصورة بين ( 1 : 20 ) وهما 10 أعداد جميعهم أعداد فردية عدا العدد ( 2 )، ويمكن استخراجهم كالتالي ( 2 – 3 – 5 – 7 – 9 – 11 – 13 – 15 – 17 – 19 )
الطريقة الثانية
بينما الطريقة الثانية لمعرفة الأعداد الأولية؛ فهي اختبار كل عدد ينحصر بين (1:20) وهل يقبل القسمة على واحد، وعلى العدد نفسه، فإذا تحقق الشرطان ويعتبر عدد أولي، وإذا لم يتحقق فيعتبر عدد مركب وليس أولي.
الأعداد الأولية من 1 إلى 1000
يمكنك معرفة الأعداد الأولية التي تنحصر بين العدد من ( 1 : 1000 ) من خلال إتباع الخطوات التالية:

- إدراج جدول وكتابة الأعداد من 1 : 1000
- اشطب العدد 1 لأنه عدد غير أولي.
- ضع دائرة حول العدد ( 2 ) لأنه العدد الأولي الزوجي الوحيد.
- انتقل للعدد 3، وضع دائرة حول الرقم لأنه أول عدد أولي فردي؛ حيث أنه يقبل القسمة على نفسه وعلى العدد واحد.
- اشطب على كل مضاعفات العدد 3 مثل الأعداد ( 6 – 12 – 24 – 48 ) لأنهم أعداد زوجية، وجميع الأعداد الزوجية ليست أولية عدد العدد ( 2 ).
- تجربة جميع الأعداد التي تقع بين 3 : 1000 وهل تقبل القسمة على نفسها وعلى الواحد، والعدد الذي تنطبق عليه الشروط يعتبر عدد أولي.
- كما يمكن شطب جميع الأعداد الزوجية عدا العدد ( 2 ) لأنه عدد أولي واختبار كل الأعداد الفردية عدا العدد ( 1 ) لأنه عدد غير أولي، والعدد الذي يقبل القسمة على واحد وعلى نفسه؛ فهو عدد أولي.
- في النهاية، ستجد أن إجمالي الأعداد الأولية المحصورة بين الأعداد من 1 : 1000 هما 168عدد.
| الأعداد من ( 1 : 1000 ) | الأعداد الأولية | إجمالي الأعداد الأولية |
| من 1 : 100 | 2/ 3/ 5/ 7/ 11/ 13/ 17/ 19/ 23/ 29/ 31/ 37/ 41/ 43/ 47/ 53/ 59/ 61/ 67/ 71/ 73/ 79/ 83/ 89/ 97 | 25 عدد أولي |
| من 101 : 200 | 101/ 103/ 107/ 109/ 113/ 127/ 131/ 137/ 139/ 149/ 151/ 157/ 163/ 176/ 173/ 179/ 181/ 191/ 193/ 197/ 199 | 21 عدد أولي |
| من 201 : 300 | 211/ 223/ 227/ 229/ 233/ 239/ 241/ 251/ 257/ 263/ 269/ 271/ 277/ 281/ 283/ 293 | 16 عدد أولي |
| من 301 : 400 | 307/ 311/ 313/ 317/ 331/ 337/ 347/ 349/ 353/ 359/ 367/ 373/ 379/ 383/ 389/ 397 | 16 عدد أولي |
| من 401 : 500 | 4010/ 409/ 419/ 421/ 431/ 433/ 439/ 443/ 449/ 457/ 461/ 463/ 467/ 479/ 487/ 491/ 499 | 17 عدد أولي |
| من 501 : 600 | 503/ 509/ 521/ 523/ 541/ 547/ 557/ 563/ 569/ 571/ 577/ 587/ 593/ 599 | 14 عدد أولي |
| من 601 : 700 | 601/ 607/ 613/ 617/ 619/ 631/ 641/ 643/ 647/ 653/ 659/ 661/ 673/ 677/ 683/ 691 | 16 عدد أولي |
| من 701 : 800 | 701/ 709/ 719/ 727/ 733/ 739/ 743/ 751/ 757/ 761/ 769/ 773) 787/ 797 | 14 عدد أولي |
| من 801 : 900 | 809/ 811/ 821/ 823/ 827/ 829/ 839/ 853/ 857/ 859/ 863/ 877/ 881/ 883/ 887 | 15 عدد أولي |
| من 901 : 1000 | 907/ 911/ 919/ 929/ 937/ 941/ 947/ 953/ 967/ 971/ 977/ 983/ 991/ 997 | 14 عدد أولي |
هل الواحد عدد أولي
العدد الأولي هو العدد الطبيعي الصحيح الأكبر من الواحد، والأعداد الأولية هي الأعداد التي لا تقبل القسمة إلا على نفسها وعلى العدد واحد فقط، لذلك فإن الواحد عدد غير أولي وغير مركب، لأنه ليس له مكان ضمن قائمة الأعداد الأولية.
اطلع على: ما هي الأعداد النسبية وغير النسبية
الأعداد الأولية من 1 إل ى 10
هي الأعداد التي تقبل القسمة على نفسها وعلى الواحد فقط.
- الأعداد الأولية المحصورة بين ( 1 : 10 ) هما ( 2/ 3 / 5 / 7 )
- إجمالي الأعداد الأولية من 1 إلى 10 هم 4 أعداد.
اطلع على: مجموع الأعداد الفردية من 1 إلى 100
الأعداد الأولية من 1 إلى 30
يمكنك تجربة قابلية القسمة على الواحد وعلى العدد نفسه، لتحديد الأعداد الأولية المحصورة بين ( 1 : 30 ) باستخدام الآلة الحاسبة أو القسمة البسيطة بالورقة والقلم أو تحليل العدد إلى عوامل، والأعداد الأولية هي ( 2/ 3/ 5/ 7/ 11/ 13/ 17/ 19/ 23)
اطلع على: العدد النسبي.. الفرق بين الأعداد النسبية والأعداد غير النسبية
الأعداد الأولية الفردية
الأعداد الفردية ليست كلها أعداد أولية، حيث أن الأعداد الأولية هي التي تقبل القسمة على نفسها وعلى العدد واحد فقط.

- العدد 2 عدد أولي بالرغم من أنه عدد زوجي لكنه يقبل القسمة على نفسه وعلى العدد واحد فقط.
- معظم الأرقام الفردية أعداد أولية؛ لذا يعتقد البعض أن جميع الأعداد الفردية أولية لكنه اعتقاد خاطئ، ويمكن التحقق من الرقم الأولي عن طريق قسمته على واحد وعلى نفسه فقط.
-
على سبيل المثال: الأعداد الأولية التي تقع بين
( 1 : 12
)
هم ( 2/ 5/ 7/ 11)
.
- بالرغم من أن العدد 9 عدد فردي إلا أنه عدد غير أولي، لأن العدد 9 يقبل القسمة على العدد واحد وعلى نفسه وعلى العدد 3
- بالرغم من أن العدد 2 عدد زوجي إلا أنه عدد أولي، لأنه يقبل القسمة على نفسه وعلى الواحد فقط.
- هذا يدل على أن الأعداد الفردية ليست كلها أعداد أولية.
اطلع على: هل 79 عدد اولي ؟ خصائص الأعداد الأولية
هل 2 عدد أولي
العدد (2) يعتبر عدد أولي لأنه لا يقبل القسمة إلا على نفسه وعلى العدد واحد فقط، وهو العدد الزوجي الأولي الوحيد.
أسهل طريقة لمعرفة العدد الأولي
هناك العديد من الطرق التي يمكن من خلالها تحديد العدد الأولي، ومنها:
- استعمال الآلة الحاسبة: يمكنك معرفة العدد الأولي عن طريق الآلة الحاسبة باستخدام علامة القسمة ÷ وتجربة إذا كان العدد يقبل القسمة على نفسه وعلى العدد واحد أم لا، فإذا تحقق الشرطان فيكون العدد أولي.
- القسمة البسيطة: تعد من أسهل الطرق للمبتدئين، وذلك من خلال استخدام ورقة وقلم وتجربة القابلية القسمة لمعرفة العدد الأولي.
- تحليل العوامل: تتم هذه الطريقة عن طريق ضرب عدد × عدد آخر للحصول على العدد المراد تحليلها، وذلك لتجزئة العدد لأعداد أصغر.
- استعمال شجرة العوامل: يمكن من خلال تلك الطريقة اكتشاف العوامل المشتركة للعدد؛ فإذا تم تحليل العدد للعاملين فقط يكون العدد أولي، أما في حالة تحليل العدد لأكثر من عاملين فيكون العدد غير أولي.
- على سبيل المثال: العدد ( 17 ) يقبل القسمة على العدد واحد (1 وعلى نفسه (17) فقط؛ لذا فهو عدد أولي.
- مثال آخر: العدد ( 4 ) يقبل القسمة على نفسه (4) وعلى العدد واحد ( 1)، كما أنه يقبل القسمة على العدد ( 2)؛ لذا فهو عدد غير أولي.
التشفير والأعداد الأولية
تعتمد بعض خوارزميات التشفير المهمة مثل RSA بشكل حاسم على حقيقة أن التحليل الأولي للأعداد الكبيرة يستغرق وقتًا طويلاً، ونُوضح فيما يلي شرح لآلية التشفير:
- في الأساس لدينا “مفتاح رئيسي” يتكون من ناتج مكون من اثنين من الأعداد الأولية .
- كما يُوجد “مفتاح سري” يتكون من هذين الأوليين المستخدمين لفك تشفير الرسالة.
- يُمكن للمبرمج جعل المفتاح عامًا بحيث يُتاح للجميع استخدامه لتشفير الرسائل التى تم إرسالها للشخص.
- معرفة العوامل الأساسية تُمكن من فك تشفير الرسائل ويّتعين على أي شخص آخر أن يُحلل الرقم، الأمر الذي يستغرق وقتًا طويلاً ليكون عمليًا، نظرًا للحالة الحالية لفن نظرية الأعداد.
- السبب في أنها أساسية تشفير RSA فعندما تضرب اثنين معًا، فإن النتيجة هي رقم لا يُمكن تقسيمه إلا إلى تلك الأعداد الأولية، ولكن عندما تستخدم أعدادًا أولية أكبر بكثير لـ p و q، فمن المستحيل إلى حد كبير على أجهزة الكمبيوتر إخراجها من N.
- هذه الحقيقة تجعلها ذات أهمية حيوية للاتصالات، حيث تعمل معظم أنظمة التشفير الحاسوبية الحديثة باستخدام العوامل الأولية للأعداد الكبيرة.
- يُمكن أن يكون العدد الكبير الذي تم استخدامه لتشفير ملف معروفًا ومتاحًا للجمهور، لأن التشفير يعمل بحيث لا يُمكن استخدام سوى العوامل الأولية لهذا العدد الكبير لفك تشفيره مرة أخرى.
- بالرغم من كون العثور على هذه العوامل من الناحية الفنية هو مجرد مسألة وقت، إلا أن الوقت المستغرق طويل لدرجة أننا نقول أنه لا يُمكن تحقيقها.
أمثلة حول الأعداد الأولية والمُركبة
العدد الأولي هو عدد صحيح موجب له عاملين بالضبط إذا أعطينا له الرمز p، فإن العوامل هي بالضرورة أن يقبل القسمة على 1 و p نفسها، وأي رقم لا يتبع هذا يُسمى بالأرقام المركبة مما يعني أنه يُمكن تحليلها في أعداد صحيحة موجبة أخرى، كما يلي:
- أول عشرة أعداد أولية: هي 2 ، 3 ، 5 ، 7 ، 11 ، 13 ، 17 ، 19 ، 23 ، 29 وتجدر الإشارة إلى أن الرقم 1 هو عدد غير أولي.
- قبل استخدام الآلات الحاسبة وأجهزة الكمبيوتر كانت تُستخدم الجداول العددية لتسجيل جميع الأعداد حتى حد معين.
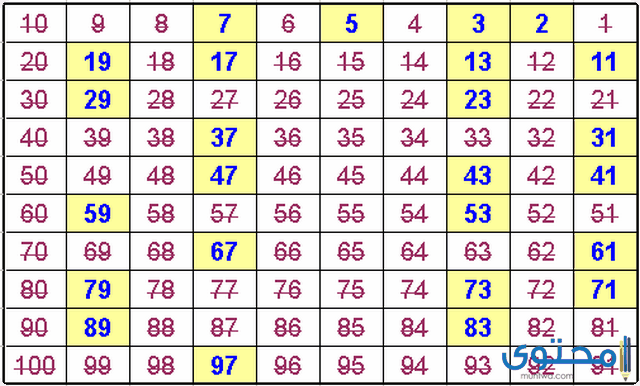
- كانت تُطبع عادةً والطريقة الأكثر شيوعًا لإنتاج قائمة تُسمى غربال إراتوستينس .
- تُنتج هذه الطريقة رسمًا تخطيطيًا يُسمى مخطط إراتوستينس ، ويُوضح الرسم البياني قائمة الأعداد الأولية حتى 100 ممثلة بواسطة المربعات الملونة.
- هي أعداد صحيحة موجبة تحتوي على عاملين فقط 1 والرقم نفسه على سبيل المثال , عوامل العدد 6 هي 1،2،3 و 6 ، وهي أربعة عوامل في المجموع.
- لكن عاملي العدد 7 هما 1 و 7 فقط، ليصبح المجموع اثنين.
- ومن ثم ، فإن 7 عدد أولي ولكن 6 ليس كذلك ، بل هو عدد مركب لكن تذكر دائمًا أن 1 ليس عددًا أوليًا ولا معقدًا.
ما هي الاعداد الأولية سؤال في غاية الأهمية يجب على جميع الأشخاص المهتمة بعلم الرياضيات معرفته، فهناك عددًا لا حصر له منها على الرغم من أنها تصبح أقل تكرارًا مع تقدمنا، فمن السهل نسبيًا العثور على أعداد أولية أكبر إلا أنه من الصعب حتمًا إعادة تحليل الأعداد الكبيرة وتحويلها إلى أولية.
