بحث عن التطابق للصف الأول الإعدادي

إذا كنت طالبًا في الصف الأول الإعدادي وتهوى مادة الهندسة أو حتى لا تهواها فقد تواجه مشكلة كبيرة في فهم درس التطابق بين المثلثات والدوائر والشروط التي تستطيع من خلالها أن تؤكد تطابق مثلثين أو الدائرتين معًا، وقد يتطلب منك الأمر أن تلاحظ ذلك بمجرد النظر وذلك من خلال زيادة حل التمارين الرياضية بجميع أشكالها.
محتوى المقال
مقدمة بحث عن التطابق
بدايةً عليك أن تعرف أن التطابق ليس فقط في المثلثات ولكن يمكن أن يكون في الدائرة أيضًا، والتطابق معناه أن كل ضلع يساوي الضلع المماثل مع ضلع آخر من حيث القياس الزوايا .
ما هي أنواع التطابق في المثلثات
التطابق يكون إما تطابق بين زاويتين أو بين ضلعين أو بين دائرتين وله أشكال متعددة هي:
- الضلع والضلع: هذا النوع من التطابق يشترط أن يكون ساقي مثلث مع ساقي مثلث آخر وأن يكون مثلثين قائمي الزاوية فهذا يعني تطابق المثلثين معًا ويتم اختصار هذه الحالة بحرفي L.
- الوتر والزاوية الحادة: معنى ذلك أن الوتر في المثلث الأول يطابق الوتر في المثلث الثاني وأن تكون إحدى الزوايا الحادة في أحد المثلثين مطابقة لإحدى الزوايا الحادة في المثلث الثاني هذا معناه تطابق المثلثين ويتم اختصار هذه الحالة بحرفي HA.
- الضلع والزاوية الحادة: هذا النوع معناه ضرورة تطابق ساق مثلث بساق المثلث الآخر وأن تكون زاويته الحادة تساوي الزاوية الحادة للمثلث الثاني، فإن هذا يعني تطابق المثلثين معًا ويتم اختصار هذه الحالة بحرفي LA.
- الوتر والضلع : تطابق المثلثين من حيث الوتر والضلع يعني أن يكون الضلع الذي يمثل وتر المثلث قائم الزاوية مطابقًا للضلع الذي يمثل وتر مثلث آخر قائم الزاوية ويتم اختصار هذه الحالة بالحرفين HL.

شاهد أيضًا: ما الكسور التي في أبسط صورة؟ وما أنواع الكسور
شروط تطابق المثلثات
وفي سياق الحديث حول بحث عن التطابق يجب أن يتوفر بعض الشروط في المثلثين حتى يقال أن هذين المثلثين متطابقين وهي:
- أن يتطابق ضلعين من أضلاع المثلثين إضافة إلى الزاوية التي توجد بينهما مع الزوايا التي تقابلها في المثلث الثاني.
- أن تتطابق زاويتان والضلع الموصل بين المثلثين مع الزاويتين والضلع المقابل لهما.
- أنّ تتساوى الـ 3 أضلاع مع 3 أضلاع المثلث الثاني هذا معناه أنهما متطابقين.
- أن يتساوى ضلع مثلث زاوية قائمة مع ضلع مثلث آخر بزاوية قائمة أيضًا وأن يتساوى وتر مثلث مع الوتر المقابل له في المثلث الثاني.
- يجب التنويه عن إن تساوي زوايا المثلث مع زوايا مثلث ثاني لا يعني أنهما متطابقين بل إنهما متشابهان وأن تطابق المثلثين لا يكون من خلال التساوي في طولهما أو عددهم.
اقرأ أيضاً: بحث عن المثلثات المتشابهة
أسئلة عن التطابق
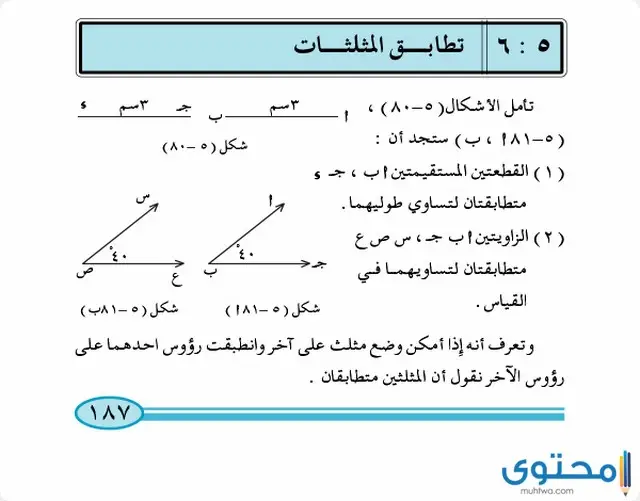
متى يصبح هناك قطعتين مستقيمتين متطابقتين؟
- إذا تساوى طول القطعتين معًا فهما متطابقتين.
متى يصبح المضلعات متطابقة؟
- يقال على المضلعات أنها متطابقة معًا في حالة تساويهما في طولها وفي حالة تساوي الزوايا المتقابلة معًا في القياس وبذلك لو وجد مربعين تطابق أحد أضلاع أحدهما مع طول ضلع المربع الآخر فهذا معناه تطابق المربعين معًا.
- أما المستطيل فتختلف معايير اعتباره متطابقًا مع مستطيل آخر قليلا عن معايير تحديد تطابق المربعين.
- معنى ذلك أن أحد أضلاع المستطيل لو تساوى في طوله وعرضه مع أحد أضلاع مستطيل ثاني فهذا يعني أنه متطابق، كما أن تطابق قياس زوايا المستطيل المتقابلة معناه أيضًا تطابق المستطيلين معًا.
شاهد أيضًا: الفرق بين المربع والمعين والمستطيل
الفرق بين تشابه المثلثات وتطابقها
ذكرنا في السطور السابقة أن أطوال أضلاع المثلثين لو تساويا أصبحا متشابهين وليسا متطابقين، فهل تعرف الفرق بين التشابه والتطابق؟
التشابه بين المثلثين هو أن يكونا متماثلين في كل شيء في أطوال الأضلاع وفي الزوايا وأنواعها، أما لو اختلف عنصر من عناصر المثلثين أصبحا متطابقين؛ هذا معناه أن يكون طول وتر المثلث الذي زاويته قائمة متساوي مع وتر مثلث آخر قائم الزاوية فهذا معناه تطابق المثلثين.
لو تساوت طول ضلعين من أضلاع مثلث مع طول ضلعين مثلث ثاني مع تساوي الزاوية التي تقع بين هذين الضلعين في المثلثين فهذا معناه تطابقهما معًا، لكن تشابه المثلثات معناه تساوي نفس قياسات زوايا المثلث بالرغم من اختلاف أحجامها وأضلاعها فهذا يعني أنهما متوافقين.
يصبح المثلثين متشابهين إذا تساوت قياسات زوايا مع قياس زاوية مثلث ثاني وأن تكون أطوال أضلاعه متوافقة شريطة أن تكون هذه الأضلاع المتوافقة هما الأضلاع الذين تقع الزاوية المتماثلة مع زاوية المثلث الثاني بينهما وهذا يعني توافق ضلعين بينهما تساوي زاويتين.
ملاحظة : يصبح المثلثين متشابهين لو تساوت قياسات زوايا أحد المثلثين مع قياسات زوايا المثلث الثاني وهذا يعني تماثل وزوايا المثلثين معًا.
قوانين هامة حول المثلثات
استكمالاً لحديثنا حول بحث عن التطابق توجد قوانين متعددة متعلقة بالمثلثات يستطيع الطالب أن يصل إليها لو كانت أطوال أضلاع المثلث هي أ-ب-ج، وقياس زوايا هذه المثلثات التي تقابل هذه الأضلاع، هي:
- القانون المسمى بقانون الجيب: أ÷جا (أ)= ب÷جا (ب)= ج÷جا (ج)
- القانون المسمى بقانون جيب التمام: 2 =ب2+ج2-2×ب×ج×جتا (أ)، أوب 2= أ2+ج2-2×أج×جتا (ب)،أوج2= ب 2+أ2-2×بأ×جتا (ج).
يجب أن تعرف أن:
- حرف الـ(أ) يرمز إلى طول الضلع الأول للمثلث وإلى الزاوية المقابلة للضلع (أ).
- حرف الـ(ب ) يرمز إلى طول ضلع المثلث الثاني وإلى الزاوية المقابلة للضلع (ب).
- أما حرف الـ (ج) فهو يرمز إلى طول الضلع الثالث للمثلث وإلى الزاوية المقابلة للضلع (ج).
فهل يمكن الآن أن تكتب بحث عن التطابق للصف الأول الإعدادي ؟ ولكن عليك التعرف على التطابق بين الدوائر لأن هذا الدرس يمكن أن يفيدك للغاية في مادة الهندسة التي تعد أساسًا لك لو كنت عاشقًا لمادة الرياضيات.

التعليقات